But what if you work for a math-heavy industry, pharmacology, medicine or sociology, and complex statistical analysis is part of your daily routine? Did you find a user-friendly data analysis tool that works on your Mac?
StatPlus:mac supports Microsoft Excel for Mac (supported versions: 2004, 2008, 2011, 2016, 2019) and Apple Numbers v3/v4/v5 as a data source. StatPlus:mac does not require Internet connection (except for optional auto-update feature). Now that we know what a two-way ANOVA is used for, we can now calculate a two-way ANOVA in Excel. To begin, open your data in Excel. If you don’t have a dataset, download the example dataset here.

StatPlus:mac turns your copy of Microsoft Excel for Mac (2004 - 2019) or Apple Numbers into a powerful statistical tool without making you learn another software or part with extraordinary amounts of money. You'll use the familiar interface to perform complex analysis and calculations, enabling you to concentrate on analyzing the results rather than figuring out how to achieve them.
ANOVA in Excel is a built-in statistical test that is used to analyze the variances. For example, when you buy a new item, we usually compare the available alternatives, which eventually helps us choose the best from all the available alternatives. The Analysis of Variance (ANOVA) has many varieties, but in essence, it has the purpose of evaluating whether factors are associated with any outcome values. And factors are categorical variables.
Upgrade Your Spreadsheet
Turn Microsoft Excel or Apple Numbers into a powerful statistical package with StatPlus:mac and perform data analysis on a Mac in the familiar environment. Stop wasting your time learning new tools and try StatPlus:mac right away.
70+ Features
StatPlus:mac allows Mac users to perform all forms of data analysis from the very basics to complex analysis, including non-parametric and regression analysis, survival and time series analysis, and a wide variety of other methods. Version 7 includes standalone spreadsheet and can be used without Microsoft Excel or Apple Numbers installed.
Multi-platform
StatPlus:mac is available for both Mac and PC platforms (PC version includes standalone and Excel add-in versions) at no extra charge. Save learning time and costs for your mixed PC and Mac environment.
Free Trial
We have free trial that gives you an opportunity to evaluate the software before you purchase it. Should you have any questions during the trial period, please feel free to contact our Support Team.
Affordable
StatPlus:mac is most affordable solution for data analysis on Mac (with Excel and Numbers support). You will benefit from the reduced learning curve and attractive pricing while enjoying the benefits of precise routines and calculations. Mac/PC license is permanent, there is no renewal charges.
Requirements
How To Do Anova On Excel Mac
StatPlus:mac requires macOS 10.9-10.15 (macOS Catalina is supported; v5 requires 10.5+). StatPlus:mac supports Microsoft Excel for Mac (supported versions: 2004, 2008, 2011, 2016, 2019) and Apple Numbers v3/v4/v5 as a data source. StatPlus:mac does not require Internet connection (except for optional auto-update feature).
Statistical features list
- Pro Features
- Standalone spreadsheet with Excel (XLS and XLSX), OpenOffice/LibreOffce Calc (ODS) and text documents support.
- 'Add-in' mode for Excel 2004, 2008, 2011, 2016 and 2019.
- 'Add-in' mode for Apple Numbers v3, v4 and v5.
- Priority support.
- Permanent license and free major upgrades during the maintenance period.
- Access to Windows version.
- Options to emulate Excel Analysis ToolPak results and migration guide for users switching from Analysis ToolPak.
- Basic Statistics
- Detailed descriptive statistics.
- One-sample t-test.
- Two-sample t-test.
- Two-sample t-test for summarized data.
- Fisher F-test.
- One-sample and two-sample z-tests.
- Correlation analysis and covariance.
- Normality tests (Jarque-Bera, Shapiro-Wilk, Shapiro-Francia, Cramer-von Mises, Anderson-Darling, Kolmogorov-Smirnov, D'Agostino's tests).
- Cross-tabulation and Chi-square.
- Frequency tables analysis (for discrete and continuous variables).
- Multiple definitions for computing quantile statistics.
- Analysis of Variance (ANOVA)
- One-way and two-way ANOVA (with and without replications).
- Three-way analysis of variance.
- Post-hoc comparisons - Bonferroni, Tukey-Kramer, Tukey B, Tukey HSD, Neuman-Keuls, Dunnett.
- General Linear Models (GLM) ANOVA.
- Within subjects ANOVA and mixed models.
- Multivariate Analysis
- Principal component analysis (PCA).
- Factor analysis (FA).
- Discriminant function analysis.
- Nonparametric Statistics
- 2x2 tables analysis (Chi-square, Yates Chi-square, Exact Fisher Test, etc.).
- Rank and percentile.
- Chi-square test.
- Rank correlations (Kendall Tau, Spearman R, Gamma, Fechner).
- Comparing independent samples
Mann-Whitney U Test, Kolmogorov-Smirnov test, Wald-Wolfowitz Runs Test, Rosenbaum Criterion. Kruskal-Wallis ANOVA and Median test. - Comparing dependent samples
Wilcoxon Matched Pairs Test, Sign Test, Friedman ANOVA, Kendall's W (coefficient of concordance). - Cochran's Q Test.
One Way Anova In Excel
- Regression Analysis
- Multivariate linear regression (residuals analysis, collinearity diagnostics, confidence and prediction bands).
- Weighted least squares (WLS) regression.
- Logistic regression.
- Stepwise (forward and backward) regression.
- Polynomial regression.
- Curve fitting.
- Tests for heteroscedasticity: Breusch–Pagan test (BPG), Harvey test, Glejser test, Engle's ARCH test (Lagrange multiplier) and White test.
- Time Series Analysis
- Data processing.
- Fourier analysis.
- Smoothing.
- Moving average.
- Analysis.
- Autocorrelation (ACF and PACF).
- Interrupted time series analysis.
- Unit root tests - Dickey–Fuller, Augmented Dickey–Fuller (ADF test), Phillips–Perron (PP test), Kwiatkowski–Phillips–Schmidt–Shin (KPSS test).
- Survival Analysis
- Life tables.
- Kaplan-Meier (log rank test, hazard ratios).
- Cox proportional-hazards regression.
- Probit-analysis (Finney and LPM).
LD values (LD50/ED50 and others), cumulative coefficient calculation. - Receiver operating characteristic curves analysis (ROC analysis).
AUC methods - DeLong's, Hanley and McNeil's. Report includes: AUC (with confidence intervals), curve coordinates, performance indicators - sensitivity and specificity (with confidence intervals), accuracy, positive and negative predictive values, Youden's J (Youden's index), Precision-Recall plot. - Comparing ROC curves.
- Data Processing
- Sampling (random, periodic, conditional).
- Random numbers generation.
- Standardization.
- Stack/unstack operations.
- Matrix operations.
- Statistical Charts
- Histogram
- Scatterplot.
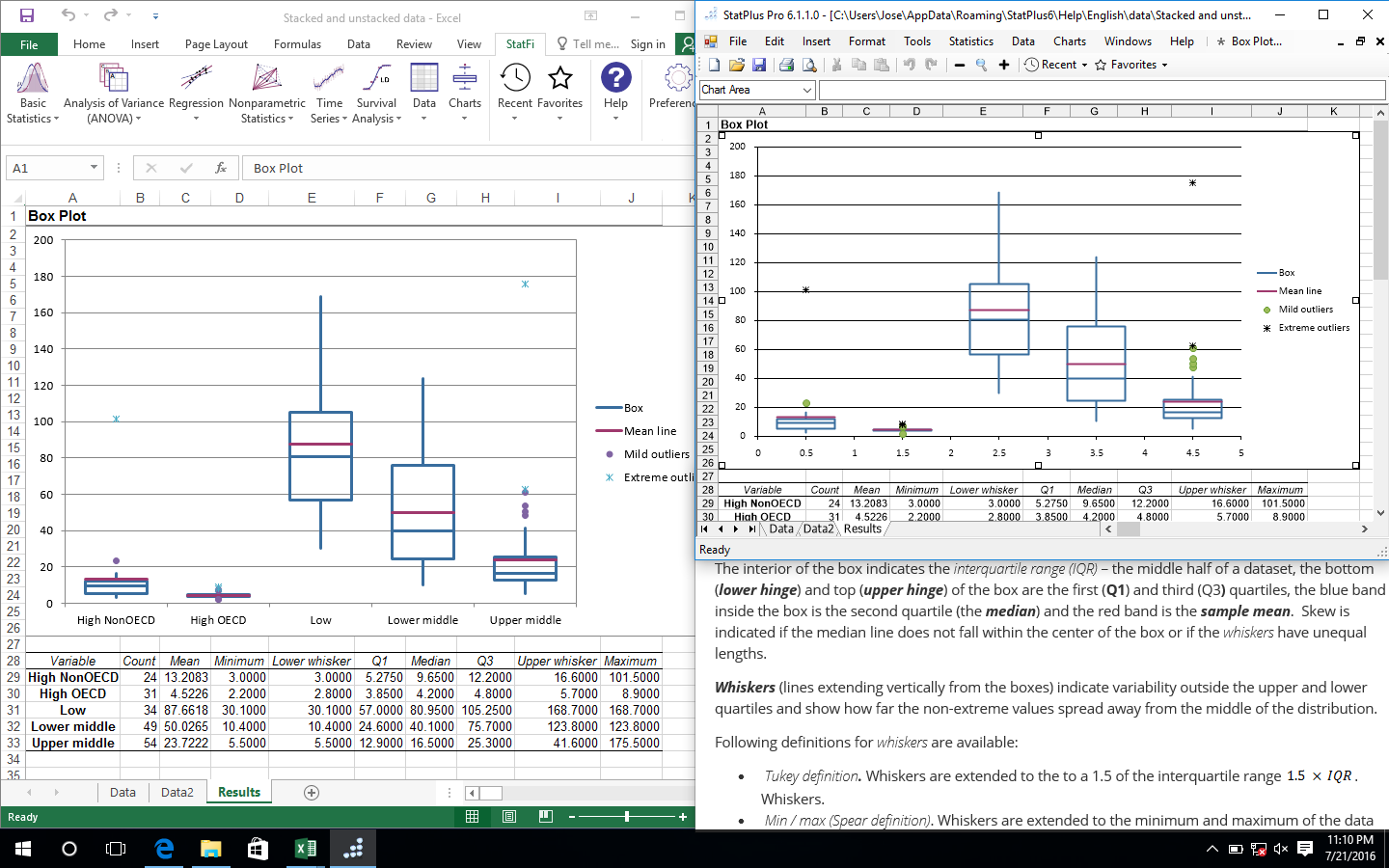
- Box plot.
- Stem-and-leaf plot.
- Bland-Altman plot.
- Bland-Altman plot with multiple measurements per subject.
- Quantile-quantile Q-Q plots for different distributions.
- Control charts - X-bar, R-chart, S-chart, IMR-chart, P-chart, C-chart, U-chart, CUSUM-chart.
From learning about the one-way ANOVA, we know that ANOVA is used to identify the mean difference between more than two groups. A one-way ANOVA is used when we have one grouping variable and a continuous outcome. But what should we do if we have two grouping variables? As you’ve probably guessed, we can conduct a two-way ANOVA. Because this situation is fairly common, I created the page below to provide a step-by-step guide to calculating a two-way ANOVA in Excel. As always, if you have any questions, please email me a MHoward@SouthAlabama.edu!
As mentioned, an ANOVA is used to identify the mean difference between more than two groups, and a two-way ANOVA is used to identify the mean difference between more than two groups when you have a two grouping variables and a continuous outcome. So, a two-factor ANOVA is used to answer questions that are similar to the following:
- What is the mean difference of test grades between left- and right-handed students, students in Dr. Howard’s and Dr. Smith’s classes, and the combinations of these groups?
- What is the mean difference in total output of factories defined by location as well as industry?
- What is the mean difference in performance for four different training programs, each performed at four different locations, and the combination of training program and location.
Also, in testing these effects, a two-way ANOVA can determine whether Variable 1 has an effect, whether Variable 2 has an effect, and whether there is an interaction between Variable 1 and Variable 2. An interaction indicates that the effect of Variable 1 depends on Variable 2 and the effect of Variable 2 depends on Variable 1. One way to think about it is: Variable 1 may have an effect, Variable 2 may have an effect, but an interaction occurs when something special happens when Variable 1 and Variable 2 are studied together. For instance, the effects may be multiplicative when studied together.
Now that we know what a two-way ANOVA is used for, we can now calculate a two-way ANOVA in Excel. To begin, open your data in Excel. If you don’t have a dataset, download the example dataset here. In the example dataset, we are simply comparing the means two different grouping variables, each with three different groups, on a single continuous outcome. The variables are Variable 1 (Group A, B, and C) and Variable 2 (Groups 1, 2, and 3). You can imagine that the groups and the outcome are anything that you want.

Before continuing, I must note that Excel is pretty bad at calculating a two-way ANOVA, so I recommend using SPSS or R instead. Nevertheless, if you need to use Excel, it can calculate a result for you.
With that noted, your dataset should look like the image below.
Like most other analyses, we want to begin by going to the Data tab and clicking on Data Analysis. If you don’t have the Data Analysis button, read my guide on how to activate Data Analysis in Excel.
Click on “Anova: Two-Factor With Replication”, then click on “OK”.
Click on the button highlighted below, which tells Excel where your data is located.
Highlight all your data AND your labels. Then press the other button highlighted below.
Now, we need to tell Excel how many participants are in our groups. As you can see above, there are two grouping variables each with three groups. This makes a total of nine groups: 1A, 2A, 3A, 1B, 2B, 3B, 1C, 2C, and 3C. In each of these groups, we have three numbers. For instance, Group 1A has values of 10, 7, and 10. This means that we have three participants per group. So, if you are using the example dataset, enter “3” in the box highlighted below.
Now your screen should look like the following. Press “OK”.
Your output should appear as the following:
Woah! That is a lot of output! Don’t worry, we will walk through it step-by-step.
First, we are going to determine whether the variable that defined our rows has a statistically significant effect. In the example dataset, this was Variable 1 (Group A, B, and C). To determine whether it was statistically signifiant, let’s first look at the F-statistic, which is our test statistic.
The F-statistic for Variable 1 was 5.127. While we would want to report it, the F-statistic doesn’t tell us a lot on its own. So, we should look at the p-value.
The p-value was .017. Because this is less than .05, we consider the effect of Variable 1 to be statistically significant. So, there is a significant difference among Groups A, B, and C.
Bluebeam tools free. Now, let’s look at Variable 2’s results (Groups 1, 2, and 3.).
The F-statistic is 1.901. Again, we should report this value, but also look at the p-value to determine how to interpret our results.
The p-value is .178. Because this is greater than .05, our result is not statistically significant. Therefore, we would say that Variable 2 does not have a significant effect, and there is not a notable difference between Groups 1, 2, and 3.
Lastly, let’s look at the interaction term.
The F-statistic is 1.660. Report this, but let’s also look at the p-value.
The p-value is .203. This result is not statistically significant, and we would therefore say that there is no significant interaction between Variable 1 and Variable 2.
Together, we know that there is a significant effect for Variable 1, but there was not a significant effect for Variable 2 or the interaction. Because Variable 1 was significant, we know that there is some type of difference between Groups A, B, and C. But how are they different?
Download firefox 47.0 1 for mac. Download Firefox 47.0.1 for Mac from FileHorse. 100% Safe and Secure One of the World`s Most Popular Web Browsers for Mac.
If we were using a more advanced program, such as SPSS or R, we could perform post hoc tests or planned comparisons. Unfortunately, Excel does not have this feature easily implemented. So, we are just going to look at the group means.
The highlighted means are for Groups A, B, and C. From looking at the means, we can tell that Group A has the highest value, followed by Group C, followed by Group B. While we don’t know whether these specific comparisons are significant, we can get a general feel for how the groups differ.
But what if Variable 2 was statistically significant? Well, we can look at the values highlighted below.
From these means, we can see that Group 3 had a slightly higher mean than Groups 1 and 2; however, because Variable 2 did not have a significant effect, these differences are not statistically significant.
Finally, if we had a significant interaction effect, we would need to look at the means of all groups. They are highlighted in the picture below.
From this image, we can see that Group C3 had a value of 10, Group A1 had a value of 9, and the groups descended from there. Because there was not a significant interaction effect, these individual group comparisons are not that meaningful.
Phew! That was a lot, but we are done now. If you have any questions or comments, please email me at MHoward@SouthAlabama.edu.
